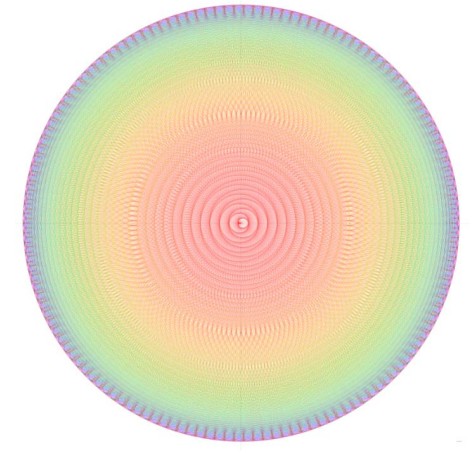
El presente artículo explora las formas que pueden tomar los valores de \( b^n \mod p \) cuando \( p \) es primo y \( b \) es la base. Se llama a \( b \) la base porque estos valores son la representación de \( 1/p \) en la base \( b \). Para visualizar estos valores, la forma natural que encontré consiste en enrollarlos sobre el círculo subdividiéndolo en \( p - 1 \) partes. Luego solo queda unir los puntos o valores sucesivos. Otra forma de ver estos valores es considerar el desarrollo decimal (en base \( b \)) de \( 1/p \) y desplazar el punto decimal hacia la derecha. Una de las figuras conocidas de esta representación es la cardioide, que representa \( 1/p \) en base 2. Lo interesante es que, al usar otras bases y variar \( p \), se descubren una multitud de dibujos extraños. El artículo explica de dónde vienen estas formas y da una fórmula para calcular por adelantado qué forma tendrá el dibujo. El artículo intenta responder una pregunta simple: si la cardioide representa el inverso de un número primo (bajo ciertas condiciones), ¿qué ocurre con otras bases como 10?
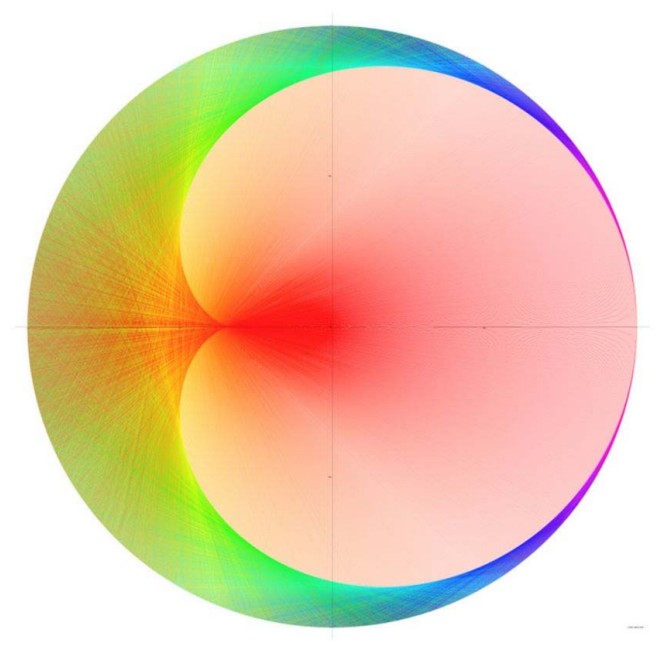
La cardioide es en realidad la representación del inverso de un número primo en base 2. La coloración de los segmentos rectos ayuda a visualizarlo: el color es proporcional a la longitud del segmento (y además, es más bonito).
El inicio de esta investigación se remonta a 1974, cuando buscaba desentrañar el misterio de los cuadrados mágicos. Uno en particular era el de Durero, bien conocido.
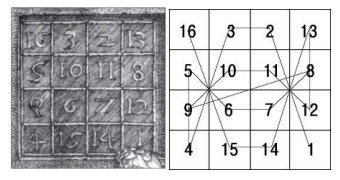
Si se conectan los valores del 1 al 16, se observa un patrón simétrico interesante. Pero lo que me dejaba perplejo eran los valores de \(10^n \mod 17\). De hecho, la secuencia de residuos de \(10^n\) módulo 17 es casi mágica:
\[ 1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12, 1, \ldots \]
Son los restos de dividir las potencias de 10 entre 17, exactamente como la división larga que se aprende en la escuela primaria. Me preguntaba si no habría alguna forma de encontrar una base y un número primo que permitiera construir un cuadrado mágico sin mucho esfuerzo, ya que los valores de \( b^n \mod p \) son fáciles de calcular. Fue entonces cuando se me ocurrió la idea de colocar estos valores en el círculo de radio 1 y ver cómo lucían.
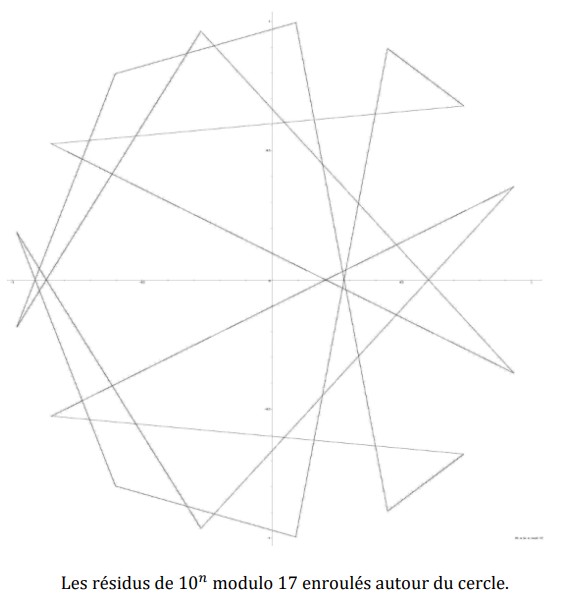
Los residuos de \(10^n\) módulo 17 enrollados alrededor del círculo.
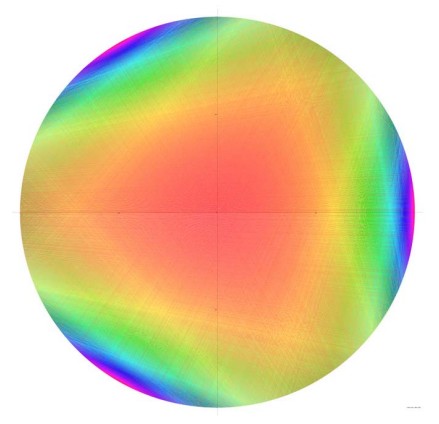
No se obtiene un cuadrado mágico, pero el dibujo es simétrico. El siguiente paso fue entonces calcular \(1/p\) en base 10, pero esta vez con \(p = 61\).
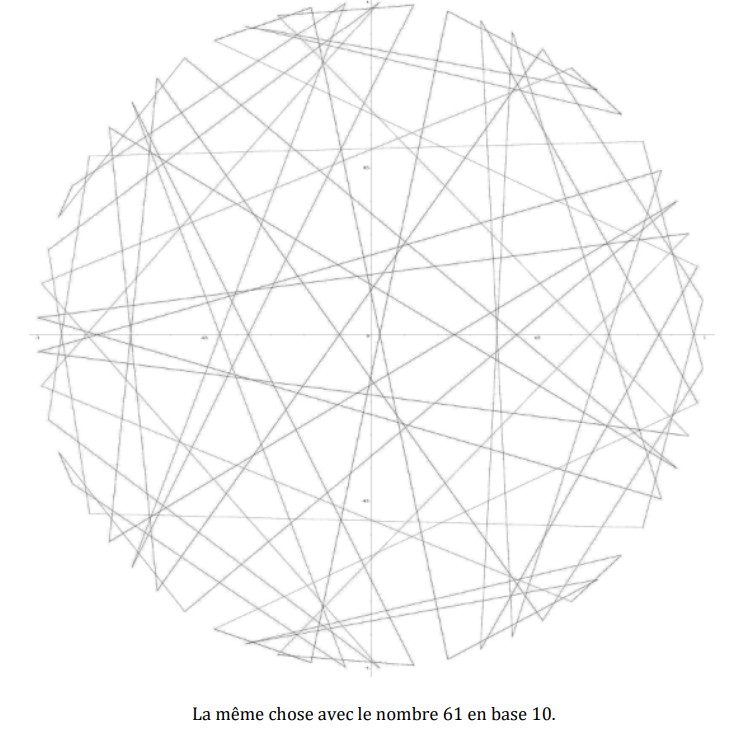
Lo mismo con el número 61 en base 10.
Luego calculé \(1/257\) en base 10 para ver qué sucedía. Elegí este primo porque la subdivisión del círculo en 256 partes es fácilmente realizable a mano (regla y compás).
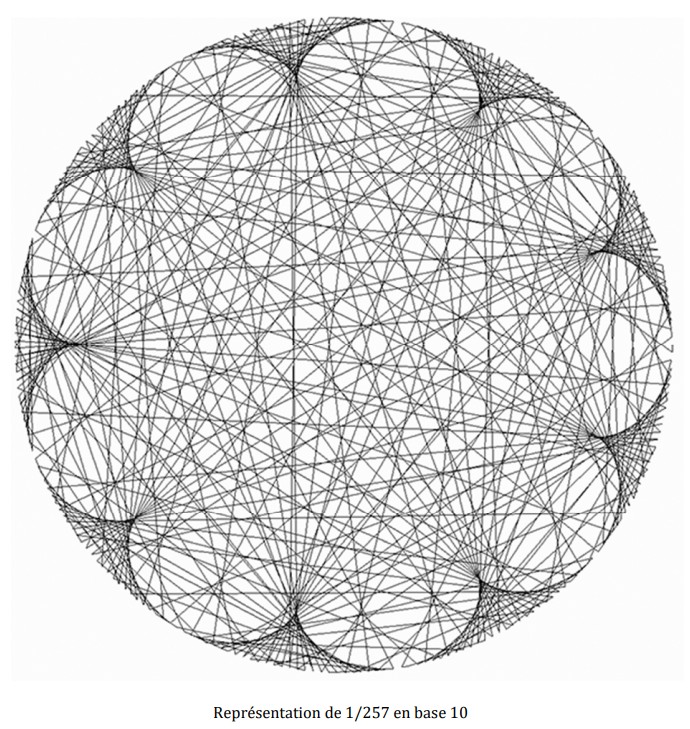
Representación de \(1/257\) en base 10
Aquí se distinguen 9 puntas; estas 9 se explican por la elección de la base 10. Cualquiera que sea el número primo, siempre habrá \( b - 1 \) puntas, siempre que \( p \) sea lo suficientemente grande como para que se vea claramente y que \( b \) sea una raíz primitiva de \( p \). La raíz primitiva de \( p \) es tal que hay \( p - 1 \) residuos módulo \( p \). Una buena pregunta, entonces, es contar cuántas puntas hay en total. Aquí se distinguen 23 puntas adicionales. ¿De dónde provienen estas 23 puntas? Repitiendo experimentos con varios primos y bases, llegué a la fórmula para el número de sub-puntas \( P_1 \), siendo \( P_0 = b - 1 \):
\[ P_1 = (1 - b) \left\lfloor \frac{b^2}{p} \right\rfloor - b + p + 1 \]
Aquí, [] representa la parte entera. Esta fórmula bastaba en la época (1979) para explicar algunos dibujos, pero no todos. Más tarde, los recursos informáticos para producir estos dibujos me permitieron explorar mucho más los valores de \( p \) y encontrar otros grupos de puntas. Por ejemplo, con \( p = 10007 \) y \( b = 107 \) se obtiene:

Zoom sobre la imagen de \(107^n \mod 10007\) (colorizada).
Llamo grupo de puntas al conjunto de picos sobre un mismo perímetro (a la misma distancia del centro del círculo). No es propiamente un grupo. Se distinguen 3 puntas en el centro, seguidas por otras 20 y 23 puntas. Un zoom a menor escala revela las 43 puntas calculadas según la fórmula:
\[ (1 - b) \left\lfloor \frac{b^2}{p} \right\rfloor - b + p + 1 \]
Queda por averiguar por qué se cuentan 20 y 23 puntas. En el dibujo completo se distinguen hasta 8 capas de puntas.

Al alejarse se distinguen las 43 puntas \( P_1 \), el dibujo de las líneas está coloreado con un color proporcional a la longitud, lo que facilita la visualización.
Lo que parece surgir es que las numerosas series de puntas se generan a partir de: \( P_0 = b - 1 \) y \( P_1 = (1 - b) \left\lfloor \frac{b^2}{p} \right\rfloor - b + p + 1 \) únicamente.
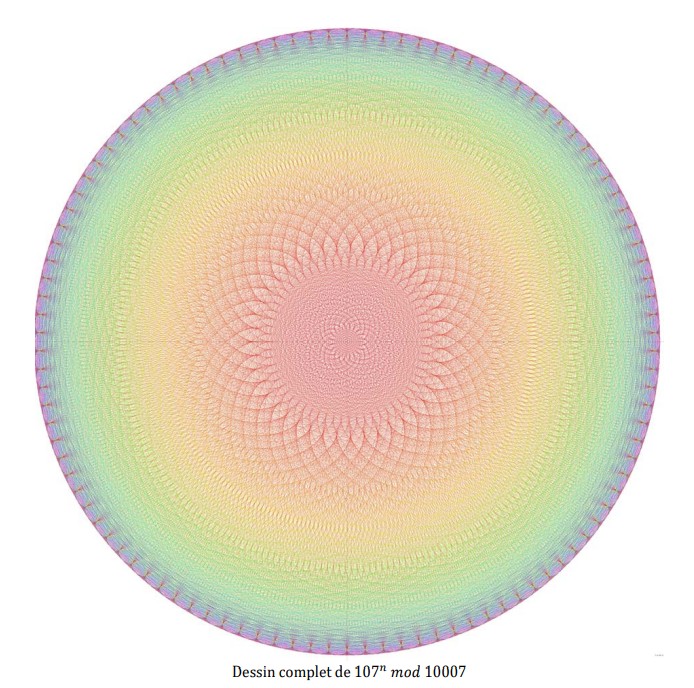
Dibujo completo de \(107^n \mod 10007\)
Las dos cantidades \( P_0 \) y \( P_1 \) bastan para explicar todos los grupos o conjuntos de puntas. Solo hace falta considerar las diferencias de los múltiplos de \( P_0 \) y \( P_1 \), es decir, el conjunto \( E_{P_0} = \{ P_0, 2P_0, 3P_0, 4P_0, \ldots \} \) y el conjunto \( E_{P_1} = \{ P_1, 2P_1, 3P_1, 4P_1, \ldots \} \), las diferencias absolutas entre ambos y tomar la lista de los valores más pequeños. Basta con tener los 10 o 20 primeros términos de estos dos conjuntos.
En nuestro caso, \( P_0 = 106 \) y \( P_1 = 43 \). Los conjuntos son:
\[ E_{P_0} = \{106, 212, 318, 424, 530, 636, 742, 848, 954, 1060, \ldots\} \] \[ E_{P_1} = \{43, 86, 129, 172, 215, 258, 301, 344, 387, 430, \ldots\} \]
Luego se calculan todas las diferencias entre cada par de elementos para obtener una lista creciente. Esta lista es la lista de los grupos de puntas.
La lista final es entonces: \( \{3, 6, 17, 20, 23, 26, 37, 40, 43, 100, 106\} \), y al eliminar los múltiplos de un mismo número, la lista depurada queda: \( \{3, 17, 20, 23, 26, 37, 40, 43, 106\} \).
Los dos números, \( P_0 = 106 \) y \( P_1 = 43 \), son entonces los generadores de los grupos de puntas que aparecen en el dibujo. También hay que comprender que hay un límite de precisión e identificación de un grupo de puntas: no siempre son visibles claramente. Para validar la hipótesis sobre \( P_0 \) y \( P_1 \), se toma una muestra de primos y bases. Para simplificar, se eligen bases que son raíces primitivas de \( p \).

Con \( 265^n \mod 1667 \), los valores de \( P_0 = 264 \) y \( P_1 = 181 \)
Tras el cálculo se obtienen los números: \( 15, 23, 38, 53, 68, 83, 98, 113, 128, 136, 151, 166, 181 \). Se logra contar un grupo de 15 puntas y otro de 38, fáciles de contar. Mucho menos visible es el grupo de 23 puntas más hacia el centro. Según el principio establecido, deberían haber 264 puntas en el perímetro del círculo y 181 puntas secundarias (\( P_1 \)), algo más alejadas. Se alcanza el límite de visibilidad, pero parece funcionar bien. Las 181 puntas son demasiado confusas para contarlas con precisión.
Existe sin embargo un límite mecánico al representar estos gráficos en un ordenador. El límite está en la cantidad de líneas simultáneas en un mismo dibujo. Con \( p = 65537 \), por ejemplo, el centro del dibujo se vuelve indescifrable. Incluso con una imagen de 32768 × 32768 (más de mil millones de píxeles), es demasiado para una sola imagen. Podría intentarse con un formato RAW mucho mayor, pero se vuelve inmanejable, incluso con Photoshop. En un solo dibujo, el límite está cerca de \( p = 100000 \).
Elegí entonces un primo bastante grande (\( p = 10037 \)) para ver todas las armónicas de estos extraños dibujos. Hay 4606 raíces primitivas de 10037. Dicho de otro modo, el número primo \( 1/10037 \) expresado con esas 4606 bases diferentes genera los dibujos. También exploré todos los primos hasta 100000 con la base 240. La hipótesis de que \( P_0 \) y \( P_1 \) bastan para explicar todas las “armónicas” se valida, ya que al tomar primos como \( P_0 = 92 \) y \( P_1 = 239 \), por ejemplo, se obtiene el mismo dibujo con las armónicas calculadas con la fórmula.
Según los cálculos, deberían aparecer los siguientes grupos de puntas: \( 1, 17, 18, 19, 20, 35, 36, 37, 38, 54, 55, 56, 57, 72 \ldots \)
Si se prueba con primos grandes, se verifica que el dibujo es el mismo y que se distinguen más y más armónicas, exactamente las que se habían anticipado.
Aquí, con \( p = 14009 \), se obtiene \( P_0 = 92 \) y \( P_1 = 239 \), y el centro del enorme dibujo de mil millones de píxeles muestra: una punta en el centro, 18 y 19 puntas.

Con otro dibujo realizado con el primo \( p = 32173 \), se obtienen claramente 55 puntas. Cuanto más grande es el número primo, más conjuntos aparecen, y el número de puntas por conjunto coincide perfectamente con la lista calculada de antemano.

Un último dibujo con el primo \( p = 45263 \) en base 240. Si se cuentan correctamente, se encuentran 92 puntas sobre el perímetro:
Está efectivamente en la lista:
\( \{1, 17, 18, 19, 20, 35, 36, 37, 38, 54, 55, 56, 57, 72, 73, 74, 75, 91, 92, 182, 239\} \)


Las 80 primeras imágenes de \( b^n \mod 10037 \)
Todas las demás imágenes están en: http://plouffe.fr/10037


La riqueza del dibujo es la misma pero con mayor precisión; no hay armónicas complejas. Si la base es, por ejemplo, 60, ya en el centro se observan muchas armónicas. En ciertos dibujos se llegan a contar hasta 10 grupos diferentes de puntas.

Aquí con \( 60^n \mod 10007 \)
4. Los grupos de puntas no son subgrupos del grupo cíclico, y esto por una buena razón: las puntas se agrupan sobre un mismo perímetro en paquetes más o menos iguales. Si habláramos de grupos y subgrupos, tendríamos una cantidad precisa de elementos, y este no es el caso.
Por ejemplo, \( 63^n \mod 10037 \) tiene en su centro 7 puntas distintas que contienen aproximadamente 1433 líneas cada una, dado que \( 10036 = 4 \cdot 13 \cdot 193 \), esto será común en la mayoría de los casos.
Las armónicas en este caso son: \( 7, 8, 13, 14, 15, 20, 21, 22, 27, 28, \ldots \)
Elegí entonces la base 240 para obtener el máximo de efectos, y con un tamaño de gráficos de hasta 32768 × 32768, lo que representa más de mil millones de píxeles.
Aquí algunos ejemplos de figuras generadas con base 240 y ciertos números primos:

Simon Plouffe 2020: base = 240, primo = 1667, \( P_1 = 6 \), armónicas = 6, 95
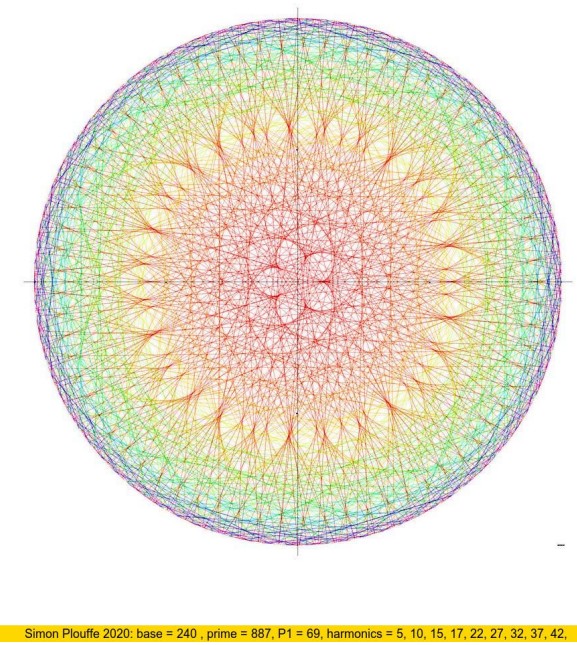
Simon Plouffe 2020: base = 240, primo = 887, \( P_1 = 69 \), armónicas = 5, 10, 15, 17, 22, 27, 32, 37, 42
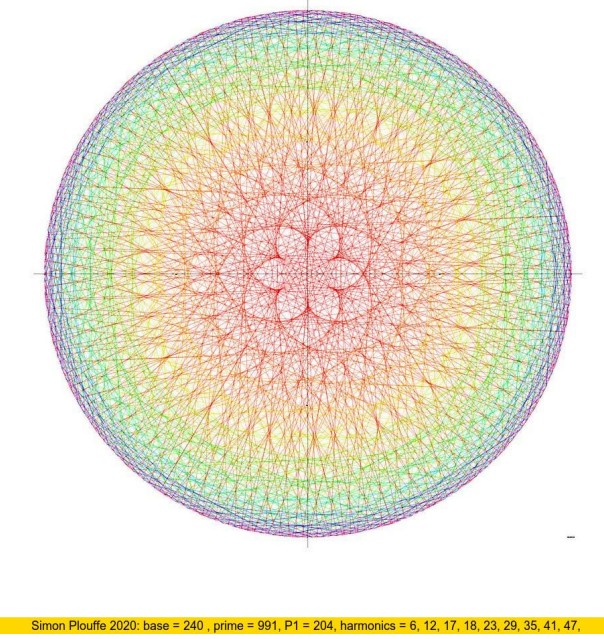
Simon Plouffe 2020: base = 240, primo = 991, \( P_1 = 204 \), armónicas = 6, 12, 17, 18, 23, 29, 35, 41, 47

Simon Plouffe 2020: base = 240, primo = 1103, \( P_1 = 92 \), armónicas = 1, 17, 18, 19, 20, 35, 36, 37, 38

Cerca del centro de \( 240^n \mod 26437 \), con colores invertidos para mejor visibilidad
\( P_0 = 239,\quad P_1 = 92 \)
El número de puntas está entre la lista de armónicas:
\( 1, 17, 18, 19, 20, 35, 37, 54, 55, 56, 57, 72, 73, 74, 75, 91, 92 \)