Existen fórmulas que parecen evidentes en su contexto original, pero que revelan una estructura profunda cuando se observan geométricamente desde una dimensión superior.
En este artículo partimos de una identidad algebraica —la fórmula de Cauchy-Binet— aplicada al determinante de Gram, $ \det(A A^t) $ y mostraremos cómo encierra el teorema de Pitágoras y la fórmula de Herón, extendidos a cualquier dimensión.
Como el siguiente documental Flatland – What the Bleep Do We Know? que muestra cómo un mundo bidimensional descubre la tercera dimensión:
La fórmula de Gram realiza un salto análogo: saca a Pitágoras y a Herón de su dimensión natural y los proyecta a espacios de dimensión arbitraria.
La fórmula de Cauchy–Binet
Se trata de una identidad puramente algebraica, válida para cualquier matriz $n\times m$, con $n$ (número de filas) menor o igual que $m$ (número de columnas), sin interpretación geométrica previa.
Ejemplo trivial.
Si $A = [a\ b]$, entonces \[ A A^t = [a^2 + b^2] \] y los menores máximos son $a$ y $b$.
La identidad se reduce a \[ a^2 + b^2 = a^2 + b^2, \] una obviedad.
Ejemplo no trivial.
Consideremos \[ A= \begin{pmatrix} 4 & -3 & -2\\ -1 & -2 & 0 \end{pmatrix}. \]
\[ A\,A^t= \begin{pmatrix} 4 & -3 & -2\\ -1 & -2 & 0 \end{pmatrix} \begin{pmatrix} 4 & -1\\ -3 & -2\\ -2 & 0 \end{pmatrix} \]El resultado ya no es evidente, la identidad funciona.
En la siguiente escena podemos comprobar la identidad con matrices aleatorias de orden 2x3.
Significado geométrico
Longitud de un vector en $\mathbb{R}^m$
Sea $u=(11,2,10)$ un vector de $\mathbb{R}^3$. Por el teorema de Pitágoras sabemos que su longitud es
\[ \|u\|=\sqrt{11^2+2^2+10^2}=15. \]
Si $A$ es la matriz con una sola fila $(11\;2\;10)$, la longitud de su vector fila, o su volumen (1-volumen), es
\[ \mathrm{vol}(A)=\sqrt{\det(A A^t)}. \]
Área de dos vectores en $\mathbb{R}^m$
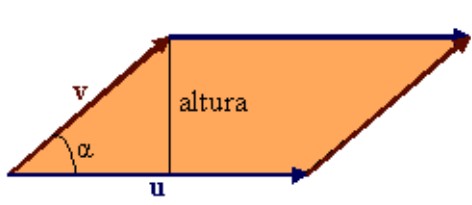
Si $u$ y $v$ son dos vectores en $\mathbb{R}^m$, el área al cuadrado del paralelogramo que determinan viene dada por:
\[ (\text{área})^2 =\|u\|^2\|v\|^2\sin^2(\alpha) =\|u\|^2\|v\|^2-(u\cdot v)^2 \]
\[ = \begin{vmatrix} u\cdot u & u\cdot v\\ v\cdot u & v\cdot v \end{vmatrix} =\det(A A^t), \]
siendo $A$ la matriz cuyas filas son los vectores $u$ y $v$. Por tanto, el área del paralelogramo es
\[ \mathrm{vol}(A)=\sqrt{\det(A A^t)}. \]
Volumen de tres vectores en $\mathbb{R}^m$
Sea $A$ la matriz cuyas filas son los vectores $u$, $v$ y $w$ de $\mathbb{R}^m$. El cuadrado del volumen del paralelepípedo que determinan es
\[ (\mathrm{vol}(A))^2 = (\text{área})^2\cdot \text{altura}^2 = \begin{vmatrix} u\cdot u & u\cdot v & 0\\ v\cdot u & v\cdot v & 0\\ 0 & 0 & \text{alt}^2 \end{vmatrix}. \]
Teniendo en cuenta que la altura puede escribirse como $\text{alt}=\alpha u+\beta v+w$, se obtiene
\[ = \begin{vmatrix} u\cdot u & u\cdot v & u\cdot\text{alt}\\ v\cdot u & v\cdot v & v\cdot\text{alt}\\ \text{alt}\cdot u & \text{alt}\cdot v & \text{alt}\cdot\text{alt} \end{vmatrix}. \]
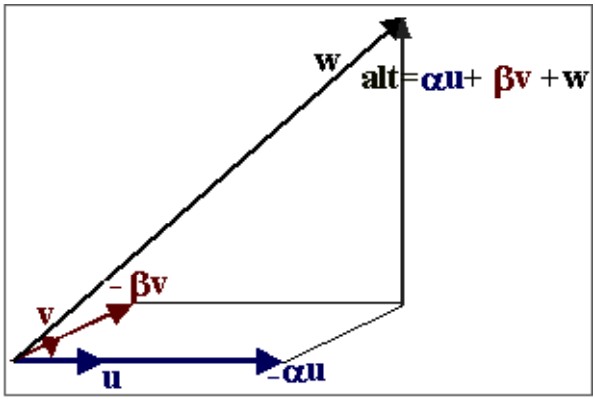
El determinante anterior coincide con
\[ \det\!\left( \begin{pmatrix} u\\ v\\ w \end{pmatrix} \begin{pmatrix} u\\ v\\ w \end{pmatrix}^{\!t} \right), \]
y concluimos finalmente que
\[ \mathrm{vol}(A)=\sqrt{\det(A A^t)}. \]
La fórmula de Herón
La fórmula de Herón permite calcular el área de un triángulo conociendo únicamente las longitudes de sus tres lados. Si un triángulo tiene lados de longitud $a$, $b$ y $c$, y denotamos por \[ s=\frac{a+b+c}{2} \] su semiperímetro, entonces su área viene dada por
\[ \text{Área}=\sqrt{s(s-a)(s-b)(s-c)}. \]
Esta expresión resulta especialmente notable porque no requiere conocer ángulos ni alturas: toda la información geométrica del triángulo queda codificada en las longitudes de sus lados.
A primera vista, la fórmula de Herón puede parecer aislada o incluso misteriosa. Sin embargo, veremos a continuación que se trata en realidad de un caso particular de la igualdad fundamental estudiada en el apartado anterior.
Herón como determinante de Gram
Consideremos una matriz $A$ con dos filas, cuyos vectores fila son $u$ y $v$. La matriz de Gram asociada es
\[ A A^t = \begin{pmatrix} u\cdot u & u\cdot v\\ u\cdot v & v\cdot v \end{pmatrix}. \]
Si denotamos \[ a=\lVert u\rVert,\qquad b=\lVert v\rVert,\qquad c=\lVert u-v\rVert, \] entonces,
\[ u\cdot v=\frac{a^2+b^2-c^2}{2}. \]
Por tanto, el determinante de la matriz de Gram toma la forma
\[ \det(A A^t)= \det \begin{pmatrix} a^2 & \dfrac{a^2+b^2-c^2}{2}\\[0.6em] \dfrac{a^2+b^2-c^2}{2} & b^2 \end{pmatrix}. \]
Esta cantidad coincide exactamente con el cuadrado del área del paralelogramo determinado por los vectores $u$ y $v$, y por tanto, con el cuadrado del doble del área del triángulo asociado.
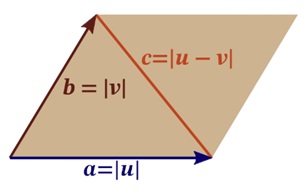
Al desarrollar el determinante, se obtiene una expresión equivalente a la fórmula de Herón que permite calcular el área de un triángulo en función de la medida de sus lados. De este modo, la fórmula clásica aparece como un caso particular de la identidad
\[ (\mathrm{Vol})^2=\det(\text{Gram}), \]
aplicada a una matriz con dos filas.
En el documento heron2.pdf puede consultarse una demostración detallada de esta equivalencia, así como su relación con el determinante de Cayley–Menger.
Volumen de un paralelepípedo y fórmula de Herón en dimensión superior
El cuadrado del volumen de un paralelepípedo determinado por varios vectores puede expresarse mediante el determinante de Gram:
\[ (\mathrm{vol}(A))^2 = \det(A\cdot A^t). \]
Esta expresión proporciona el volumen del paralelepípedo en función de la medida de sus lados y de las diagonales de sus caras, constituyendo una extensión natural de la fórmula de Herón a dimensiones superiores.
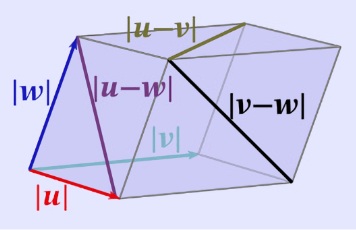
Veámoslo con más detalle. Sea $A$ una matriz de tres filas, cuyos vectores fila son $u$, $v$ y $w$. La matriz de Gram asociada es
\[ A A^t = \begin{pmatrix} u\cdot u & u\cdot v & u\cdot w\\ u\cdot v & v\cdot v & v\cdot w\\ u\cdot w & v\cdot w & w\cdot w \end{pmatrix}. \]
Por tanto,
\[ \det(A A^t) = \det \begin{pmatrix} uu & uv & uw\\ uv & vv & vw\\ uw & vw & ww \end{pmatrix}. \]
Denotemos
\[ uu=a^2,\quad vv=b^2,\quad ww=c^2, \] \[ (u-v)^2=d_1^2,\quad (u-w)^2=d_2^2,\quad (v-w)^2=d_3^2. \]
Utilizando la identidad
\[ u\cdot v=\frac{u^2+v^2-(u-v)^2}{2}, \]
se obtiene
\[ uv=\frac{a^2+b^2-d_1^2}{2},\qquad uw=\frac{a^2+c^2-d_2^2}{2},\qquad vw=\frac{b^2+c^2-d_3^2}{2}. \]
De este modo, el volumen del paralelepípedo puede calcularse únicamente a partir de las longitudes de sus aristas y de las diagonales de sus caras.
Este determinante coincide, salvo un factor constante, con el determinante de Cayley–Menger asociado:
\[ \det(A A^t) = \frac{1}{8} \det \begin{pmatrix} 0 & 1 & 1 & 1 & 1\\ 1 & 0 & a^2 & b^2 & c^2\\ 1 & a^2 & 0 & d_1^2 & d_2^2\\ 1 & b^2 & d_1^2 & 0 & d_3^2\\ 1 & c^2 & d_2^2 & d_3^2 & 0 \end{pmatrix}. \]
Concluimos así que la identidad
\[ (\mathrm{vol}(A))^2=\det(A A^t) \]
constituye una fórmula de Herón generalizada para paralelepípedos en dimensión arbitraria, siendo el orden de la matriz $A$ el que determina la dimensión del volumen considerado.
Pitágoras en cualquier dimensión
La suma de los cuadrados de los menores de orden máximo actúa como una extensión natural del teorema de Pitágoras.
Esta afirmación, que generaliza de manera directa el teorema clásico de Pitágoras, aparecerá más adelante como un caso particular de una construcción válida en cualquier dimensión.
La igualdad fundamental que utilizaremos es
\[ (\mathrm{vol}(A))^2 := \sum (\text{menores de orden máximo de } A)^2. \]
Cuando la matriz $A$ tiene una sola fila, este enunciado coincide exactamente con el teorema de Pitágoras para la longitud de un vector en el plano. Cuando el número de filas aumenta, la misma expresión describe áreas y volúmenes en dimensiones superiores.
El caso elemental: un vector en el plano
Si la matriz $A$ tiene una sola fila y dos columnas, entonces $A$ representa un vector del plano, que escribiremos como $u=(u_1,u_2)$. En este caso, los menores de orden máximo de $A$ coinciden exactamente con las coordenadas del vector.
Escribir \[ (\mathrm{vol}(A))^2 = u_1^2 + u_2^2. \]
es decir que el cuadrado de la longitud del vector $u$ es la suma de los cuadrados de sus componentes. Reconocemos aquí el teorema clásico de Pitágoras.
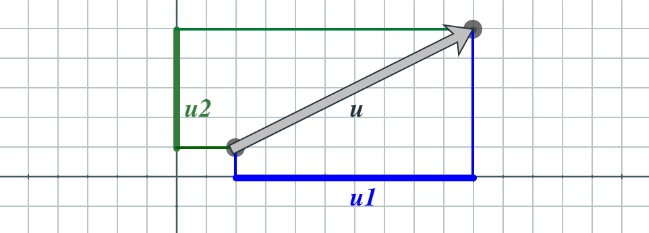
En la figura se observa que el vector $u$ se descompone en sus proyecciones sobre los ejes coordenados. La contribución de cada proyección aparece elevada al cuadrado, y su suma determina completamente la longitud del vector.
De este modo, el teorema de Pitágoras puede entenderse como el primer caso de una construcción general: el cuadrado del elemento de volumen se obtiene como suma de los cuadrados de sus proyecciones.
Dos vectores en el espacio
Consideremos ahora una matriz $A$ con dos filas y tres columnas. Sus filas representan dos vectores del espacio, \[ u=(u_1,u_2,u_3), \qquad v=(v_1,v_2,v_3), \] que determinan un paralelogramo en $\mathbb{R}^3$. En este caso, el elemento de volumen es el área de dicho paralelogramo.
El cuadrado del área viene dado por el segundo miembro de la igualdad de Cauchy–Binet, es decir, por la suma de los cuadrados de los menores de orden máximo de $A$:
\[ (\mathrm{vol}(A))^2 = \sum (\mathrm{men}_2(A))^2. \]
Geométricamente, esta expresión tiene una interpretación muy clara: cada menor de orden $2$ representa el área orientada de la proyección del paralelogramo sobre uno de los planos coordenados $x=0$, $y=0$ o $z=0$.
\[ (\text{Área})^2 = (\text{Área}_{xy})^2 + (\text{Área}_{xz})^2 + (\text{Área}_{yz})^2. \]
En la figura se muestra el paralelogramo determinado por los vectores $u$ y $v$ y sus proyecciones sobre los tres planos coordenados. El área total del paralelogramo queda completamente determinada por las áreas de estas proyecciones.
Si \[ A= \begin{pmatrix} 0 & -1 & 1\\ -1 & 1 & 1 \end{pmatrix}, \] el cuadrado del área del paralelogramo determinado por sus filas viene dado por
\[ (\mathrm{área}(A))^2 = \sum (\mathrm{men}_2(A))^2. \]
Los menores de orden $2$ de $A$ corresponden a las proyecciones sobre los planos coordenados y se obtienen eliminando, respectivamente, la columna $x$, la columna $y$ y la columna $z$:
\[ \left(\det \begin{pmatrix} 0 & -1\\ -1 & 1 \end{pmatrix} \right)^2 + \left(\det \begin{pmatrix} 0 & 1\\ -1 & 1 \end{pmatrix} \right)^2 + \left(\det \begin{pmatrix} -1 & 1\\ 1 & 1 \end{pmatrix} \right)^2. \]
\[ = (0\cdot 1 - (-1)(-1))^2 + (0\cdot 1 - 1(-1))^2 + ((-1)\cdot 1 - 1\cdot 1)^2 \]
\[ = (-1)^2 + (1)^2 + (-2)^2 = 1 + 1 + 4 = 6. \]
Por tanto, el cuadrado del área del paralelogramo gris es $6$, y su área vale $\sqrt{6}$.
Este ejemplo muestra explícitamente que el cuadrado del área de un paralelogramo es la suma de los cuadrados de las áreas de sus proyecciones sobre los planos $x=0$, $y=0$ y $z=0$.
De este modo, el teorema de Pitágoras se extiende al caso del área: el cuadrado del área de un paralelogramo es la suma de los cuadrados de las áreas de sus proyecciones. Este resultado puede considerarse un teorema de Pitágoras para áreas, válido para dos vectores en cualquier dimensión.
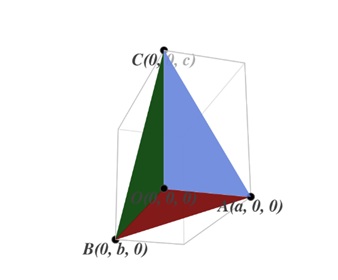
Un caso particular especialmente ilustrativo es el siguiente. Al escoger tres valores positivos para a, b y c, se dibuja el triángulo determinado por los puntos \((a,0,0)\), \((0,b,0)\) y \((0,0,c)\). Este triángulo es la mitad del paralelogramo determinado por los vectores diferencia \((a,0,-c)\) y \((0,b,-c)\), colocado con origen en el punto \((0,0,c)\).
Al aplicar la fórmula estudiada, el cuadrado del área de este triángulo resulta ser igual a la suma de los cuadrados de las áreas de sus proyecciones sobre los planos coordenados. Dicho de otro modo, en un tetraedro rectángulo, el cuadrado del área de la cara hipotenusa es igual a la suma de los cuadrados de las áreas de las tres caras cateto.
RESUMEN
Identidad de Cauchy–Binet
\[ \det(A A^t) = \sum (\text{menores de orden máximo de } A)^2 \]
Cálculo del volumen de un $n$-paralelepípedo
\[ (\mathrm{Vol}_n)^2 = \det(A A^t) \]
Permite calcular el volumen a partir de las longitudes de las aristas
y de las diagonales de sus $2$-caras.
Es la fórmula de Herón generalizada.
Pitágoras generalizado
\[ (\mathrm{Vol}_n)^2 = \sum (\text{menores de orden máximo de } A)^2 \]
Nota histórica
La identidad \[ \det(A A^t)=\sum (\text{menores de orden máximo de }A)^2 \] es un caso particular de la fórmula de Cauchy–Binet, establecida a comienzos del siglo XIX por Jacques Binet y Augustin-Louis Cauchy. Dicha fórmula expresa el determinante de un producto de matrices rectangulares en función de los menores de esas matrices y constituye una de las identidades fundamentales del álgebra lineal ( Cauchy–Binet).
Al aplicar esta identidad al producto \(A A^t\), aparece aquí la matriz formada por los productos escalares entre los vectores fila de \(A\), o matriz de Gram ( Gram matrix).
A lo largo del siglo XIX, el determinante de esta matriz —el determinante de Gram— adquirió una interpretación geométrica clara: representa el cuadrado del elemento de volumen del paralelepípedo generado por un conjunto de vectores en \(\mathbb{R}^n\). Esta lectura conecta la identidad algebraica con problemas clásicos de medida, independencia lineal y geometría métrica ( MacTutor – J. P. Gram).
Desde este punto de vista, la fórmula de Cauchy–Binet proporciona un marco unificador en el que el teorema de Pitágoras y la fórmula de Herón aparecen como casos particulares de una misma estructura algebraica y geométrica. La expresión del área o del volumen únicamente en función de longitudes se generaliza en dimensión arbitraria mediante determinantes, en particular a través del determinante de Cayley–Menger ( Cayley–Menger).
Referencias
- Geometría del determinante: apunte con escenas y explicaciones sobre el determinante y volumen en espacios de dimensión arbitraria. Determinantes.pdf
- Demostración de la fórmula de Cauchy–Binet (enlace general con prueba esquemática): definición, expresión y una demostración básica de la fórmula. Wikipedia: Fórmula de Cauchy–Binet
- Detailed proof of the Cauchy–Binet formula (algebraic proof in PDF form): provides a formal demonstration of the formula using multilinear algebra. The Cauchy–Binet formula (academic PDF)
- La unidad didáctica de UNAM, que sirve como base del contenido de este artículo: escenas interactivas, visualizaciones y explicaciones sobre volumen en ℝⁿ. UNAM – Volumen en ℝⁿ
- ProofWiki: Cauchy–Binet Formula, en inglés, con enunciados y variantes formales de la fórmula. ProofWiki – Cauchy–Binet Formula
- PlanetMath: Cauchy–Binet formula, explicación matemática de la identidad enunciada de forma canónica. PlanetMath – Cauchy–Binet formula
- Otras referencias académicas (libros clásicos de álgebra lineal donde aparece la fórmula de Cauchy–Binet): por ejemplo Shafarevich & Remizov, Linear Algebra and Geometry, §2.9 y §10.5.